Đã đăng vào thg 1 14, 1:17 CH 8 phút đọc

Big O

Big O là ngôn ngữ và thước đo để mô tả độ hiệu quả của thuật toán. Việc không hiểu rõ Big O có thể ảnh hưởng nghiêm trọng đến khả năng phát triển thuật toán của bạn. Không chỉ bị đánh giá thấp nếu không hiểu rõ Big O, bạn còn gặp khó khăn trong việc đánh giá khi nào thuật toán của mình nhanh hơn hoặc chậm hơn.

Trong học thuật:

Big O mô tả giới hạn trên (upper bound) của thời gian chạy thuật toán.
Ví dụ, một thuật toán in tất cả các giá trị trong một mảng có thể được mô tả là , nhưng cũng có thể được mô tả là: $O(N)$ , $O(N^2)$ , $O(N^3)$ , $O(2^N)$ .Điều này có nghĩa là thuật toán ít nhất nhanh bằng hoặc nhanh hơn những giới hạn này.

Trong ngành công nghiệp (và các buổi phỏng vấn), khái niệm Big O thường được dùng để mô tả một cách chặt chẽ về thời gian chạy(runtime).

Làm thử một phép so sánh

Hãy tưởng tượng kịch bản sau: bạn có một tệp trên ổ cứng và cần gửi nó cho một người bạn ở đầu kia đất nước. Bạn cần gửi tệp đó nhanh nhất có thể. Vậy bạn nên làm thế nào?

Hầu hết mọi người sẽ nghĩ ngay đến việc gửi qua email, FTP, hoặc một hình thức truyền điện tử nào đó. Đây là ý tưởng hợp lý, nhưng chỉ đúng một phần.

Nếu tệp nhỏ:

Bạn hoàn toàn đúng. Truyền điện tử sẽ nhanh hơn. Việc ra sân bay, lên máy bay và giao tận tay có thể mất từ 5 đến 10 giờ.
Nếu tệp cực lớn:

Nhưng nếu tệp thực sự rất lớn thì sao? Có thể việc vận chuyển vật lý bằng máy bay sẽ nhanh hơn không?

Câu trả lời là có! Một tệp có dung lượng 1 terabyte (1 TB) có thể mất hơn một ngày để truyền điện tử. Trong trường hợp này, bay qua cả nước để giao tệp sẽ nhanh hơn nhiều. Nếu tệp của bạn thực sự gấp (và không bị giới hạn về chi phí), bạn có thể chọn cách này.
Nếu không có chuyến bay:

Giả sử không có chuyến bay nào, bạn phải tự lái xe qua cả nước. Thậm chí ngay cả trong trường hợp này, với một tệp rất lớn, việc lái xe giao tệp vẫn có thể nhanh hơn việc truyền điện tử, do hạn chế về băng thông.

Time Complexity

Đây là ý nghĩa của khái niệm thời gian chạy tiệm cận (asymptotic runtime), hay còn gọi là Big O time. Ta có thể mô tả thời gian chạy của "thuật toán" truyền dữ liệu như sau:

Truyền điện tử:

Thời gian chạy là $O(s)$ , trong đó $s$ là kích thước của tệp. Điều này có nghĩa là thời gian truyền tệp tăng tuyến tính theo kích thước của tệp.

(Đúng là đây là một sự đơn giản hóa, nhưng đủ tốt để minh họa khái niệm này.)
Vận chuyển bằng máy bay:

Thời gian chạy là $O(1)$ với kích thước tệp. Khi kích thước của tệp tăng lên, thời gian để vận chuyển vẫn không thay đổi. Thời gian ở đây là một hằng số.

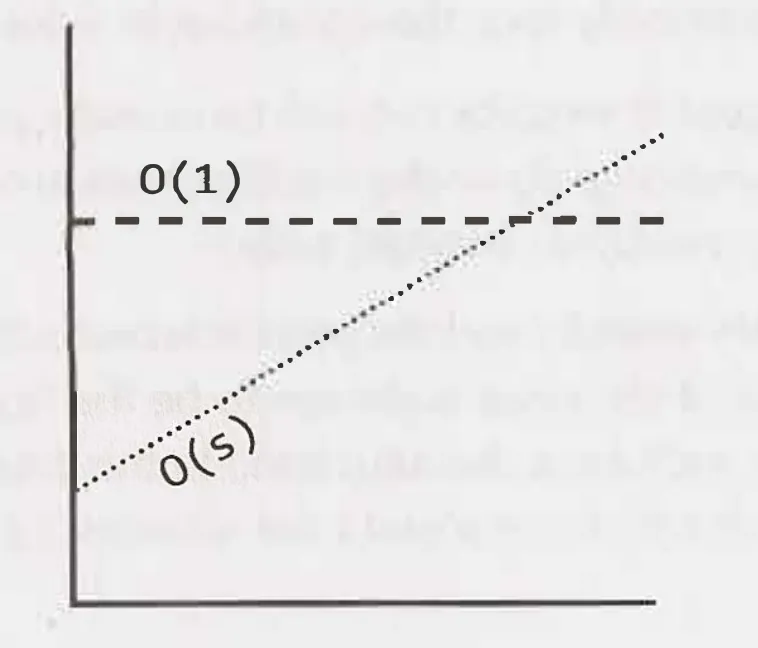
Có rất nhiều kiểu thời gian chạy (runtime) phổ biến trong phân tích thuật toán, chẳng hạn:

$O(log⁡N)$ : Logarit
$O(Nlog⁡N$ ): Tuyến tính nhân logarit
$O(N)$ : Tuyến tính
$O(N2)$ : Bình phương tuyến tính
$O(2N)$ : Lũy thừa

Space Complexity

Không chỉ thời gian, lượng bộ nhớ (memory/space) mà một thuật toán sử dụng cũng là một yếu tố quan trọng cần quan tâm.

Space Complexity là lượng bộ nhớ cần thiết để thuật toán chạy hoàn chỉnh, bao gồm:

Không gian cố định (Fixed Part): Không gian sử dụng để lưu trữ các biến, hằng số và kích thước không đổi trong suốt chương trình.
Không gian biến đổi (Variable Part): Không gian cần để lưu trữ dữ liệu thay đổi như:
- Các mảng, danh sách (arrays, lists).
- Không gian dùng cho các lời gọi hàm đệ quy (recursive calls).

Bỏ qua các hằng số

Big O tập trung vào cách thời gian chạy của một thuật toán mở rộng theo kích thước của đầu vào(input) khi nó tăng lên, đồng thời bỏ qua các hằng số và các thuật ngữ bậc thấp. Điều này là do những chi tiết này có tác động không đáng kể đến hành vi mở rộng của thuật toán khi kích thước đầu vào lớn lên.

Ví dụ: $O(2N)$ và $O(N)$ đều phát triển tuyến tính, vì vậy chúng ta coi như $O(N)$ .

Bỏ các Thành Phần Không Chiếm Ưu Thế

Bạn nên xử lý biểu thức như $O(N² + N)$ như thế nào? Phần N thứ hai không hoàn toàn là một hằng số. Nhưng nó cũng không quan trọng lắm.

Chúng ta đã nói rằng chúng ta bỏ qua các hằng số. Vì vậy, O(N² + N²) sẽ trở thành O(N²). Nếu chúng ta không quan tâm đến hằng số N² đó, thì cũng không cần quan tâm đến N. Chúng ta không cần.

Recursive Runtimes:

Đây là một ví dụ phức tạp về độ phức tạp thời gian của một hàm đệ quy.

int f(int n) {
    if (n <= 1) {
        return 1;
    }
    return f(n - 1) + f(n - 1);
}

Giải thích về độ phức tạp thời gian (Runtime):

Đối với câu hỏi này, rất nhiều người sẽ thấy hai lần gọi f và nghĩ đến O(N²). Điều này hoàn toàn sai. Thay vì đưa ra những giả định, chúng ta sẽ xác định độ phức tạp bằng cách phân tích chi tiết qua từng bước của mã.

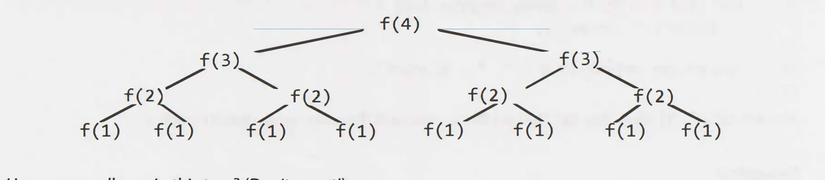
Giả sử chúng ta gọi f(4). Điều này sẽ dẫn đến việc gọi f(3) hai lần. Mỗi lần gọi f(3) tiếp tục gọi f(2), và cứ như vậy cho đến khi đạt đến f(1).

Sơ đồ cây gọi đệ quy:
- Gọi f(4) sẽ dẫn đến f(3) hai lần.
- Mỗi lần gọi f(3) sẽ dẫn đến hai lần gọi f(2).
- Mỗi lần gọi f(2) sẽ dẫn đến hai lần gọi f(1).

Như vậy, chúng ta có thể nhận thấy rằng số lượng nút (hoặc cuộc gọi) sẽ tăng gấp đôi ở mỗi cấp độ của cây gọi đệ quy.

Biểu đồ sẽ có độ sâu N.
Mỗi cấp độ có số lượng cuộc gọi gấp đôi so với cấp độ trước đó.

Do đó, tổng số nút tại mỗi cấp độ là:

$2^0 + 2^1 + 2^2 + 2^3 + \ldots + 2^N = 2^N$

Nghĩa là, độ phức tạp thời gian của f(n) là O(2^n).

Giải thích chi tiết:

$O(2^n)$ : Mỗi bước gọi đệ quy sẽ nhân đôi số lượng cuộc gọi trong cây đệ quy.
Không gian: Do có $0(2^N)$ nút trong cây tổng thể, nhưng chỉ có O(N) nút tồn tại tại một thời điểm cụ thể (các nút ở các cấp độ trước đã hoàn thành), do đó không gian sẽ là O(N).

Tóm lại:

Độ phức tạp thời gian của f(n) là $O(2^n)$ , và độ phức tạp không gian là O(N).

Nội dung được trích từ sách: Cracking the Coding Interview book