[DSA] Binary Heaps, Priority Queue
Binary Heaps
Giới thiệu
Binary heaps giống là complete binary tree (là cây nhị phân được điền đầy đủ ở tất cả các mức từ trái sang phải, ngoài trừ có thể mức cuối cùng), nó có một số tính chất sau:
- Max Heap: các node cha luôn lớn hơn node con.
- Min Heap: các node cha nhỏ hơn node con.
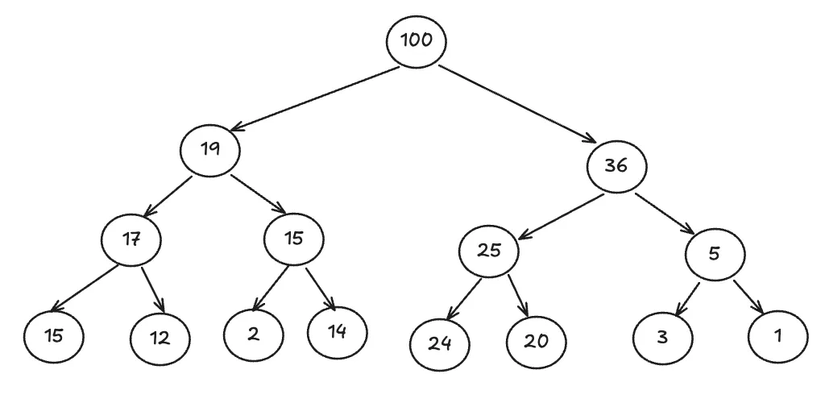
Binary Heap có thể được biểu diễn dưới dạng array như sau:

Cách xác index của các node cha và con trong 1 array độ như sau:
- Nếu 1 node nằm index n:
- Node con bên trái được lưu ở vị trí: 2n + 1
- Node con bên phải: 2n + 2
- Vị trí của node cha nếu node con nằm ở index n (làm tròn xuống): (n-1)/2
Khởi tạo
class MaxBinaryHeap {
values;
constructor() {
this.values = [];
}
insert(element) {}
bubbleUp() {}
extractMax() {}
sinkDown() {}
}
Khởi tạo các method
insert
insert(element) {
this.values.push(element);
this.bubbleUp();
}
bubbleUp() {
let idx = this.values?.length - 1;
let element = this.values[idx];
while (idx > 0) {
const parentIdx = Math.floor((idx - 1) / 2);
const parentElement = this.values[parentIdx];
if (element < parentElement) break;
this.values[idx] = parentElement;
this.values[parentIdx] = element;
idx = parentIdx;
}
}
extractMax
Trả về giá trị gốc (lớn nhất) → Thay giá trị gốc bằng phần tử cuối cùng của Heap → Sắp xếp lại heap cho đúng.
extractMax() {
const max = this.values[0];
const end = this.values.pop();
this.values[0] = end;
this.sinkDown();
return max;
}
sinkDown() {
let idx = 0;
let element = this.values[idx];
const length = this.values.length;
while (true) {
element = this.values[idx];
const leftChildIndx = 2 * idx + 1;
const rightChildIndx = 2 * idx + 2;
const leftChildElement = this.values[leftChildIndx];
const rightChildElement = this.values[rightChildIndx];
let swap = null;
if (leftChildIndx < length) {
if (leftChildElement > element) {
swap = leftChildIndx;
}
}
if (rightChildIndx < length) {
if (
(rightChildElement > element && !swap) ||
(swap && rightChildElement > leftChildElement)
) {
swap = rightChildIndx;
}
}
if (!swap) break;
this.values[idx] = this.values[swap];
this.values[swap] = element;
idx = swap;
}
}
Độ phức tạp
| Method | Big O |
|---|---|
| Insertion | O(log N) |
| Removal | O(log N) |
| Search | O(N) |
Priority Queue
Là kiểu dữ liệu giống queue nhưng được sắp xếp dựa vào độ ưu tiên.
Ở đây ta sẽ sử dụng Binary Heap để xây dựng Priority Queue
Khởi tạo
class PriorityQueueNode {
value;
priority;
constructor(value, priority) {
this.value = value;
this.priority = priority;
}
}
class PriorityQueue {
values: PriorityQueueNode[];
constructor() {
this.values = [];
}
enqueue(value, priority) {}
bubbleUp() {}
dequeue() {}
sinkDown() {}
}
Khởi tạo các method
enqueue
enqueue(value, priority) {
const newNode = new PriorityQueueNode(value, priority);
this.values.push(newNode);
this.bubbleUp();
}
bubbleUp() {
let idx = this.values?.length - 1;
let element = this.values[idx];
while (idx > 0) {
const parentIdx = Math.floor((idx - 1) / 2);
const parentElement = this.values[parentIdx];
if (element.priority < parentElement.priority) break;
this.values[idx] = parentElement;
this.values[parentIdx] = element;
idx = parentIdx;
}
}
dequeue
dequeue() {
const max = this.values[0];
const end = this.values.pop();
this.values[0] = end;
this.sinkDown();
return max;
}
sinkDown() {
let idx = 0;
let element = this.values[idx];
const length = this.values.length;
while (true) {
const leftChildIndx = 2 * idx + 1;
const rightChildIndx = 2 * idx + 2;
element = this.values[idx];
const leftChildElement = this.values[leftChildIndx];
const rightChildElement = this.values[rightChildIndx];
let swap = null;
if (leftChildIndx < length) {
if (leftChildElement.priority > element.priority) {
swap = leftChildIndx;
}
}
if (rightChildIndx < length) {
if (
(!swap && rightChildElement.priority > element.priority) ||
(swap && rightChildElement.priority > leftChildElement.priority)
) {
swap = rightChildIndx;
}
}
if (!swap) break;
this.values[idx] = this.values[swap];
this.values[swap] = element;
idx = swap;
}
}
All rights reserved